Il trasporto dei fluidi è uno degli aspetti più importanti nella progettazione di un impianto chimico. Dimensionare correttamente le tubazioni di un impianto ha un enorme impatto in termini di costi: si stima infatti che mediamente più del 10% del capitale investito nella progettazione di un nuovo impianto sia dovuto alle sole tubazioni.
Concetti base
Il comportamento macroscopico di un fluido tra i punti 1 e 2 di un condotto rappresentato da un volume di controllo fisso, può essere espresso, dopo opportune semplificazioni e assunzioni, attraverso la seguente equazione di bilancio di energia meccanica:
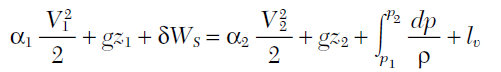(Eq. 1)
Che è una semplificazione dell’equazione di Bernoulli. In tale equazione:
- α è un fattore correttivo che tiene conto del fatto che il profilo di velocità può variare. In caso di moto laminare α=2, mentre se il moto è turbolento, in una tubazione il valore tende a 1.07. Tuttavia, generalmente tale valore lo si assume pari a 1 (profilo di velocità perfettamente uniforme);
- V è la velocità del fluido nei punti considerati;
- g esprime l’accelerazione di gravità;
- z è l’elevazione a cui si trova il fluido;
- δWs è il lavoro compiuto da/verso una macchina rotativa (pompa, compressore, turbina…);
- lv esprime l’energia meccanica persa dal fluido per dissipazione, per unità di massa;
- Infine, p e ρ rappresentano rispettivamente la pressione è la densità del fluido considerato.
L’equazione di Bernoulli così scritta è adatta sia a fluidi comprimibili che incomprimibili. Semplificando ulteriormente l’equazione, assumendo il fluido incomprimibile, la si può riscrivere come:
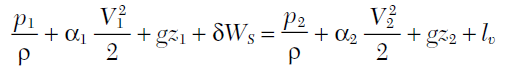(Eq. 2)
Perdite distribuite
L’ultimo termine dell’equazione, lv, esprime come detto l’energia meccanica persa per attrito dal fluido ed assumendo il circuito pari ad una tubazione, può essere descritto come somma di due componenti, una prima, dovuta alle perdite distribuite uniformemente lungo tutto il tratto di tubazione, e una seconda, dovuta a strizioni, curve, valvole e orifizi, che causano perdite concentrate in un tratto limitato del condotto. Entrambe le componenti possono essere convenientemente espresse in termini di un fattore di attrito, dipendente dalle proprietà del fluido e della tubazione. In questo modo è possibile calcolare le perdite di carico distribuite con la seguente formula di Darcy:
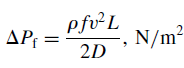(Eq. 3)
dove con D e L sono espressi rispettivamente diametro e lunghezza della tubazione (in m), e con f è indicato il fattore di attrito. Il fattore di attrito qui rappresentato è il fattore di Darcy, ma tra i processisti di estrazione chimica è utilizzato molto spesso anche il fattore di Fanning, 4 volte inferiore (l’equazione 3 di cui sopra va quindi moltiplicata per 4, se espressa con il fattore di Fanning). Il valore del fattore di attrito cambia a seconda del regime in cui si trova il fluido (laminare, in regime di transizione o turbolento) e sopratutto è funzione della rugosità del condotto, ed è l’unico valore che deve essere determinato sperimentalmente.
Fortunatamente, grazie a Colebrook e White, oggigiorno siamo in possesso di una eccellente equazione che ci consente di determinare il coefficiente di attrito senza dover ricorrere a numerose prove empiriche:
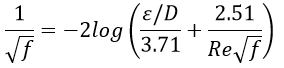(Eq. 4)
dove:
- f esprime il coefficiente di attrito di Darcy;
- ε/D il coefficiente di scabrezza relativa;
- Re è il numero di Reynolds.
La correlazione di Colebrook-White ha l’unico svantaggio di essere espressa in forma implicita. La sua risoluzione richiede quindi un procedimento ricorsivo, ma grazie alle enormi capacità computazionali dei computer di oggi, la determinazione del fattore di attrito è pressochè immediata. In alternativa è possibile ricorrere al diagramma di Moody, che riporta il fattore di attrito di Darcy calcolato con la correlazione di Colebrook-White in funzione del numero di Reynolds, o a formule approssimate, come per esempio la formula di Serghide, che ha il vantaggio di calcolare il coefficiente di attrito senza dover ricorrere ad un procedimento iterativo.
Il valore di rugosità varia a seconda del materiale. I valori medi più utilizzati sono di solito i seguenti:
| Materiale della tubazione | Rugosità (m) |
|---|---|
| Acciaio commerciale nuovo | 4.57 x 10^-5 |
| Acciaio arrugginito | 1 x 10^-2 |
| Tubi cementati | 1.5 x 10^-4 |
| Plastica | 1.52 x 10^-6 |
| Vetro | 1.7 x 10^-6 |
| Tubi galvanizzati | 1.52 x 10^-4 |
In caso di moto laminare (ovvero per Re<2300), è possibile determinare facilmente il fattore di attrito di Darcy, esso si riduce infatti a f=64/Re.
Perdite concentrate e lunghezze equivalenti
Se lungo la tubazione sono presenti curve, valvole, orifizi o riduzioni, tutti elementi che ostacolano il cammino del fluido, andrà considerata anche la perdita di carico concentrata nel punto in cui il fluido incontra l’ostacolo. Per calcolare tale perdita i metodi più utilizzati sono due: il criterio delle lunghezze equivalenti e quello delle altezze cinetiche. Mi limiterò a descrivere brevemente il primo.
Con il criterio delle lunghezze equivalenti, ogni perdita di carico concentrata incontrata dal fluido, è calcolata con la stessa formula di Darcy vista sopra, in cui la perdita concentrata è considerata pari a quella distribuita che avrebbe il fluido, se dovesse percorrere un tratto maggiorato di tubazione, lungo Li.
In questo modo, conoscendo i valori tabulati delle perdite equivalenti per i vari tipi di valvola, orifizi e curve, è possibile calcolare rapidamente la perdita di carico totale del fluido. Le lunghezze equivalenti per ogni elemento di linea sono spesso espresse in funzione del diametro della tubazione.
Di seguito ho raccolto in una tabella i valori delle lunghezze equivalenti dei principali elementi di linea con la lunghezza equivalente espressa in termini di numero di diametri. Il valore di lunghezza equivalente sarà quindi pari al diametro nominale della tubazione moltiplicato per il coefficiente moltiplicativo K riportato in tabella.
| Elemento | K = L/D |
|---|---|
| Valvola a saracinesca standard, 100% aperta | 13 |
| Valvola gate, 50% chiusa | 160 |
| Valvola a sfera > 2'', completamente aperta | 45 |
| Valvola a disco, completamente aperta | 340 |
| Check valve, swing | 135 |
| Check valve, ball | 150 |
| Curva a gomito 90°, standard | 30 |
| Curva a 45° | 20 |
| Tee, diritto | 20 |
| Tee, immissione | 65 |
| Strainer a Y | 250 |
| Uscita da recipiente | 32 |
Esempio
Di seguito un esempio illustrativo.
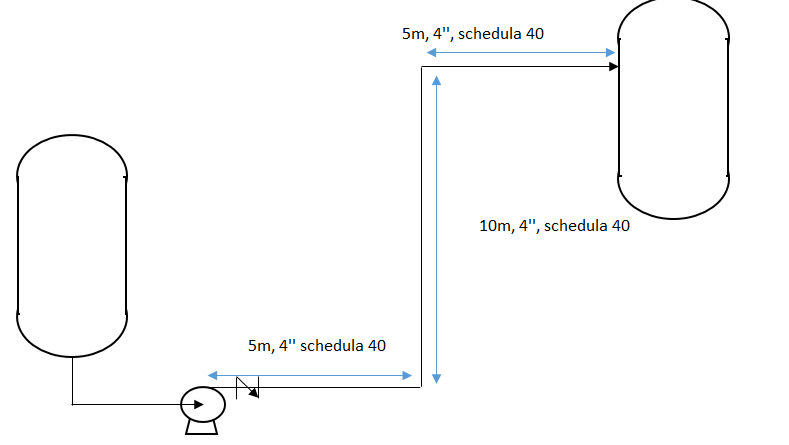
Vogliamo calcolare la prevalenza minima che dovrà fornire la pompa, per pompare acqua a temperatura di 10°C (densità 1000 kg/m3, viscosità 1.31 cp) al secondo serbatoio. La portata della pompa mostrata nel disegno è 60 m3/h. Oltre alle informazioni riportate nel disegno, ipotizziamo che siano presenti anche due curve a 90° di raggio standard. La tubazione è in acciaio commerciale (rugosità di 4.57 x 10^-5 m). Come estrema semplificazione, supponiamo che il livello di liquido nel tank di partenza sia pari a 5 metri, trascurando le perdite nella tubazione di mandata, e che entrambi i tank siano a pressione atmosferica.
La lunghezza totale del tratto di tubo è: 20 metri, con 10 di elevazione. La tubazione ha diametro esterno 4” con schedula 40, il che corrisponde ad un diametro interno di 4.026” (102.26 mm). Con questo diametro, il fluido scorre ad una velocità di 2.03 m/s. Il numero di Reynolds con la velocità appena determinata risulta pari a: 157400, moto turbolento.
Una volta noto il numero di Reynolds, il coefficiente di Darcy, iterando la formula di Colebrook-White (o utilizzando il diagramma di Moody), da come risultato: 0.0191. Possiamo quindi già calcolare le perdite di carico distribuite, applicando la formula di Darcy: 7704 Pa, ovvero 0.07704 bar.
Le perdite di carico concentrate sono dovute a due curve a 90° (L/D=30), e una check valve (L/D=135), per un totale di L=(30+30+135)*0.102=19.89 m di lunghezza equivalente. Le perdite di carico concentrate sono quindi pari circa a quelle distribuite = 7392 Pa. Il totale delle perdite di carico del circuito è pari a: 7704 + 7392 = 15096 Pa, 0.15 bar.
Per dimensionare la pompa possiamo ora applicare l’equazione di Bernoulli. Entrambi i tank si trovano a pressione atmosferica, il che vuol dire che i termini P1 e P2 si elidono. La velocità nel primo tank è pari a 0, mentre all’imbocco del secondo è pari a 2.03 m/s, e la differenza di altezza vale 5 metri (49050 Pa). La pressione che dovrà fornire la pompa sarà quindi pari a 49050+15096+2060= 66200 Pa (0.66 bar), che corrisponde ad una prevalenza di circa 7 metri.