The release of the latest version of Stockfish, version 17, has not brought significant Elo gains. Although in autotuning and with highly unbalanced opening suites, the program seems to be around 50 Elo points stronger than version 16, in reality, most well-known rating lists (CCRL/CEGT/SP-CC…) agree that the actual increase is much smaller. In fact, if using non-biased openings, it is almost negligible.
This result bring me to wonder if we are reaching a limit, beyond which, unregardless of computing power or the time given to the engine for each move, the performance improvements have become marginal.
This raises a fundamental question: have we reached a point where, even with enormous computational resources or extended time for each move, we no longer see a significant improvement?
If so, this stagnation could be due to the fact that engines like Stockfish are coming closer to a sort of “perfect play.” After solving most critical positions, only marginal details remain, which require enormous resources to improve but do not produce tangible differences in the final outcome. At a certain point, additional calculation depth no longer leads to better moves but only confirms those previously chosen.
To determine if this phenomenon is real, I decided to conduct tests using a set of non-biased openings, initially comparing Stockfish 17 with itself at progressively increasing time intervals. In addition to Stockfish 17, I later decided to include Crystal 8 and Stockfish 15.1 in the test pool. The reason for this choice is twofold: on one hand, a curiosity to see how Crystal—a derivative engine of Stockfish highly valued for game analysis—performs, as it has certain code modifications that slightly weaken it in pure strength but allow it to solve positions that Stockfish either cannot or takes much longer to solve. On the other hand, to have engines with different playing styles, which is why I added Stockfish 15.1. It has a similar strength to its more recent counterpart, but a distinct playing style, thanks to a neural network of different size and different training methods.
Chosen openings
To avoid excessively unbalanced starting positions, I selected 12 classic, balanced openings, each limited to a maximum of three moves:
- Open Game
- Queen’s Gambit
- Slav Defense
- Ruy Lopez
- Sicilian Defense
- English Opening
- Caro-Kann
- Pirc Defense
- Reti Opening
- King’s Indian Defense
- Nimzo-Indian Defense
- West Indian Defense
The engines faced each other, playing each opening once as White and once as Black.
The suite of openings in EPD format is downloadable by clicking here: openings10.epd
Thinking time and computation power
The test was conducted under the limit of 40 moves per X seconds, with an initial X value of 5 seconds, which was doubled each time, up to a reflection time 1024 times greater. Specifically, the intervals are as follows:
- x1 = 40 moves in 5 seconds, 256MB hash
- x2 = 40 moves in 10 seconds, 256MB hash
- x4 = 40 moves in 20 seconds, 256MB hash
- x8 = 40 moves in 40 seconds, 256MB hash
- x16 = 40 moves in 80 seconds, 256MB hash
- x32 = 40 moves in 160 seconds, 512MB hash
- x64 = 40 moves in 320 seconds, 512MB hash
- x128 = 40 moves in 640 seconds, 512MB hash
- x256 = 40 moves in 1280 seconds, 1024MB hash
- x512 = 40 moves in 2560 seconds, 1024MB hash
- x1024 = 40 moves in 5120 seconds, 1024MB hash
I couldn’t go further due to hardware limitations.
As for the available computing power, the tests were conducted with the Threads=1 option, using a PC with a Core i7 12700 CPU.
The test was conducted using CuteChess, and the results were calculated with the Ordo 1.0 program by Miguel Ballicora.
Test results
Below is the rating list obtained using the Ordo 1.0 software. For each engine, the reflection time used is indicated (for example: Stockfish 17 x8 used a reflection time of 40 moves in 40 seconds repeatedly). In addition to the three engines listed previously, I added others to estimate the actual playing strength.
The starting Elo rating is set to 3550 for Stockfish 11, with a fixed time of 40 moves every 80 seconds repeatedly. This is comparable, for the PC used in these tests, to 40 moves in 120 minutes repeatedly on a hypothetical Pentium 90 MHz. I use this unusual “unit of measure” to anchor the rating to a value that provides results comparable to those obtained in the past when programs were also tested against human players.
As a cross-check, I ran some tests with the older Rebel 6, also on a PC emulating the performance of a Pentium 90. The rating obtained, about 2430 Elo, is comparable to the rating achievable by the program on an actual P90 (accounting for margins of error and different openings).
# PLAYER : RATING ERROR POINTS PLAYED (%) 1 Stockfish 17 x512 : 3971 22 179.5 336 53.4% 2 Stockfish 17 x1024 : 3970 23 150.0 288 52.1% 3 Stockfish 17 x256 : 3968 22 156.0 288 54.2% 4 Crystal 8 x1024 : 3963 30 60.5 120 50.4% 5 Stockfish 15.1 x1024 : 3961 32 60.0 120 50.0% 6 Stockfish 17 x128 : 3960 22 173.0 323 53.6% 7 Crystal 8 x512 : 3959 26 84.5 168 50.3% 8 Stockfish 15.1 x512 : 3953 27 82.0 168 48.8% 9 Stockfish 17 x64 : 3950 20 231.5 406 57.0% 10 Stockfish 15.1 x256 : 3950 24 96.5 192 50.3% 11 Crystal 8 x256 : 3940 23 121.0 240 50.4% 12 Crystal 8 x128 : 3936 22 110.0 216 50.9% 13 Crystal 8 x64 : 3932 20 199.0 360 55.3% 14 Stockfish 15.1 x128 : 3924 29 84.0 144 58.3% 15 Stockfish 17 x32 : 3914 17 326.5 549 59.5% 16 Stockfish 15.1 x32 : 3898 21 183.5 312 58.8% 17 Crystal 8 x32 : 3893 20 203.0 360 56.4% 18 Stockfish 15.1 x64 : 3888 23 141.0 240 58.8% 19 Stockfish 17 x16 : 3887 18 363.5 572 63.5% 20 Stockfish 17 x64 MultiPV=4 : 3871 22 116.0 216 53.7% 21 Stockfish 15.1 x16 : 3852 19 295.5 480 61.6% 22 Stockfish 17 x8 : 3829 19 245.5 452 54.3% 23 Stockfish 15.1 x8 : 3824 21 226.0 384 58.9% 24 Crystal 8 x16 : 3821 19 221.0 432 51.2% 25 Stockfish 17 x32 MultiPV=4 : 3810 23 98.0 216 45.4% 26 Stockfish 15.1 x4 : 3760 21 230.0 408 56.4% 27 Crystal 8 x8 : 3759 19 258.0 480 53.8% 28 Stockfish 17 x16 MultiPV=4 : 3749 22 127.5 288 44.3% 29 Stockfish 17 x4 : 3749 19 266.0 504 52.8% 30 Crystal 8 x4 : 3688 23 153.5 312 49.2% 31 Stockfish 15.1 x2 : 3677 17 364.0 696 52.3% 32 Stockfish 17 x8 MultiPV=4 : 3662 22 123.5 360 34.3% 33 Stockfish 17 x2 : 3643 21 273.5 528 51.8% 34 Crystal 8 x2 : 3588 21 213.5 456 46.8% 35 Stockfish 15.1 : 3553 21 210.0 432 48.6% 36 Stockfish 11 (40/80s) : 3550 26 191.0 480 39.8% 37 Stockfish 17 : 3536 24 216.5 528 41.0% 38 Crystal 8 : 3453 28 123.0 384 32.0% 39 Gull 3 : 3192 44 90.5 312 29.0% 40 Laser 1.7 : 3187 72 29.0 120 24.2% 41 Rybka 2.3.2 : 2919 72 62.5 120 52.1% 42 Ice 4 : 2851 70 60.5 288 21.0% 43 Naraku : 2586 99 24.5 72 34.0% 44 Rebel 6 : 2432 103 11.0 120 9.2% White advantage = 45.51 +/- 2.18 Draw rate (equal opponents) = 87.55 % +/- 0.77
Interpretation of the results
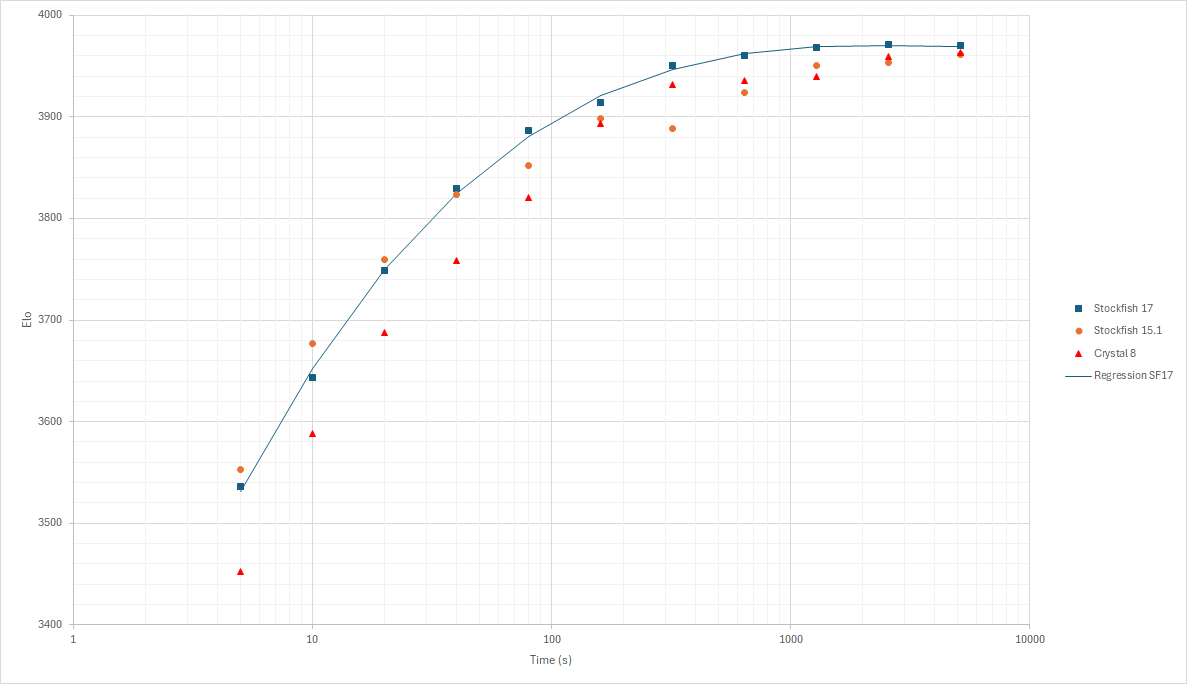
The following graph shows the Elo increase as calculation time increases.
As shown in the table, the Elo ratings exhibit an initially increasing trend as thinking time increases for each engine, highlighting a correlation between the time available per move and the engine’s performance. However, despite the margin of error, after a certain threshold, this increase in Elo rating tends to stabilize around a value of approximately 3960-3970 Elo. This is clearly reflected in the results obtained for the x512 and x1024 sets, where the Elo values of Stockfish 17, Stockfish 15.1, and Crystal 8 tend to converge.
It is interesting to note that while both Crystal 8 and Stockfish 15.1 score lower than Stockfish 17 at shorter times (as expected), the gap between the three programs tends to narrow until they almost coincide. Furthermore, as the thinking time increases, the victories of one engine over another also decrease, to the point where, with the engines assigned 512 times the initial thinking time, all games resulted in draws unregardless of the opening, and the difference in strength between the engines was determined against weaker versions of themselves.
I also conducted a test with the MultiPV=4 mode activated to see if, as reflection time increases, using multiple main variations considered by the program could enhance the program’s strength. What is observed is that this increase in strength does not actually occur, and the results of the programs with MultiPV=4 activated align with the same programs without the MultiPV option and with a thinking time of a quarter, or are even weaker, excluding truly minimal reflection times (40 moves in less than 10 seconds or even less). Indeed, even though the MultiPV option allows simultaneous consideration of multiple variations, the engine must divide its computing resources among these lines, reducing the time dedicated to each variation. Therefore, while MultiPV mode can be useful for quickly evaluating alternatives, analyzing a single line proves to be more effective for maximizing the engine’s performance over longer time controls.
This test seems to confirm that with balanced openings, increasing the thinking time does not lead to further strength increases in the engine, but instead reaches a plateau. Beyond a certain amount of time, engines are no longer able to translate the additional time into significant improvements in their position, reaching an asymptote in terms of their playing strength.
Furthermore, the test suggests that even weaker engines, when given sufficient computing time, reach the same limit.
At least for Stockfish and its main variants, this limit appears to be around 3950-4000 Elo.
These tests were conducted in single-core mode, so the effect of multi-core analysis on engine performance remains to be evaluated. The use of multiple cores makes the calculation process non-deterministic, as each core performs independent evaluations on different portions of the game tree, extending the search window. This leads to greater variability in results, which could potentially improve the engine’s performance. However, I do not believe the outcome would deviate significantly from the limit of around 4000 Elo.